

25083 - 새싹
복붙으로 1트만에 성공
중간중간 ' " / \ 를 신경쓰긴 했다.
----
1000 - A + B

'입력'받은 다음, '출력'하는 '프로그램'을 작성하는 것이 었다.
-> 정해진 범위 안의 변수를 다 넣었을 때 굴러갈 수 있는 지
input과 split을 이용하는 거였는데, 별 생각 안하고 내가 A,B = 꼴로 정리해서 그냥 프린트 했었다.
input에서 split으로 받을 경우, 컴마로 입력하는 게 아니라 공백으로 띄워서 입력해야 한다.
input으로 입력받으면 반드시 문자열 형태이므로, int로 수정해서 더하는 방식으로 해야한다.
5트만에 성공
|
1
2
|
|
A, B = input().split()
print(int(A)+int(B))
|
cs |
----
이 문제를 풀고 나서 몇 챕터의 몇 번째 문제를 풀었는지 입력하면
진척도가 프린트 되도록 하는 코드를 split을 이용해 짜보고 싶어졌다.
----
전체 단계, 전체 문제 수 = 52 테마, 385 문제

단계가 넘어갈 때 마다 elif문, 각 단계의 문제 수를 p_th에 더하는 걸로 생각을 했는데,
52가지의 테마와 문제 수를 일일히 쓸거면 코딩을 왜 배운거야..
----
range, 리스트를 이용해서 각 단계의 총 문제수를 넣어주기로 했다.

이거 range 쓰는게 맞는 걸까..?
p_th에 단순히 p_step_n의 몇 번째를 더해서는 불가능하다.
차수가 거듭할 수록 리스트의 순서대로 합을 만드는 방법이 필요하다고 생각이 들었다.
----

그때 그때 s가 p_step에 따라 p_step_n의 순서에 맞게 나오게는 해놓았다.
이제 합을 구해야 하는데...
뇌가 멈출 것 같아서 시그마를 구현하는 방법을 찾아 보았다.
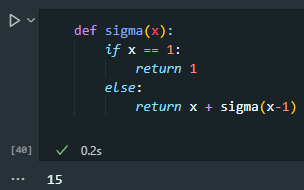
그리고 시행착오 끝에

내가.. 해냈어..
그렇게 바로 적용해서
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
p_step_n = [13,7,14,7,3,10,8,6,5,5,10,7,9,12,8,16,5,5,6,7,9,7,4,7,16,7,5,9,7,4,6,4,8,6,7,3,5,8,8,6,10,5,6,8,4,5,5,12,11,7,8,10]
def sigma(x):
if x == 1:
return 0
elif x == 2:
return p_step_n[0]
else:
return sigma(x-2) + p_step_n[x-2] + p_step_n[x-3]
p_step, p_th = input('몇 단계의 몇 번째 문제를 마지막으로 풀었는가? :').split()
p_solved = (sigma(int(p_step)) + int(p_th))
p_left = 385 - (sigma(int(p_step)) + int(p_th))
p_per = round(((sigma(int(p_step)) + int(p_th))/385) * 100, 1)
print(f'{p_step}번 테마의 {p_th}번째까지 총 {p_solved}개 풀었어.\n앞으로 {p_left}개의 문제가 남았어. ({p_per}%) ')
|
cs |
아는게 부족해서 복잡하게 한 것 같긴 하지만, 처음으로 유용한 결과물을 만들어냈다.
단계별로 리스트에서 문제 총 수를 추출해서 그 직전 단계까지의 총합을 구하는 게 관건이었다.
그리고 생각 했던 것과는 다르게 이용하지 않을 코드들도 많았고, 간단하게 표현할 방법도 따로 있었다.
첫 코딩 성공!
1번 테마의 5번째까지 풀었어.
앞으로 380개의 문제가 남았어. (1.3%)
'PS > BOJ' 카테고리의 다른 글
| (백준, 파이썬) 새롭지만 어려운 것 (0) | 2022.05.26 |
|---|---|
| (백준, 파이썬) 45분 이전에 구워진 오븐 치킨 세개 (0) | 2022.05.25 |
| (백준, 파이썬) 여러개 + 첫 현강 (0) | 2022.05.24 |
| (백준, 파이썬) 1001 (0) | 2022.05.23 |
| (백준, 파이썬) 첫 시작 (0) | 2022.05.21 |